Trong các thuật toán machine learning nói chung, và trong deep learning nói riêng, các mô hình học cách dự đoán đầu ra từ đầu vào thông qua các ví dụ trong tập dữ liệu huấn luyện.
Các điểm dữ liệu đôi khi được đo đạc với những đơn vị khác nhau, m và feet chẳng hạn. Hoặc có hai thành phần (của vector dữ liệu) chênh lệch nhau quá lớn, một thành phần có khoảng giá trị từ 0 đến 1000, thành phần kia chỉ có khoảng giá trị từ 0 đến 1 chẳng hạn. Lúc này, chúng ta cần chuẩn hóa dữ liệu trước khi thực hiện các bước tiếp theo. (theo https://machinelearningcoban.com/general/2017/02/06/featureengineering)
Các trọng số của mô hình được khởi tạo từ các giá trị ngẫu nhiên nhỏ và được cập nhật bằng thuật toán tối ưu trong quá trình backward, việc cập nhật dựa trên lỗi dự đoán (loss) trong quá trình huấn luyện.
Vì các trọng số nhỏ của mô hình nhỏ và được cập nhật dựa vào lỗi dự đoán nên việc scale giá trị của đầu vào X và đầu ra Y của tập dữ liệu huấn luyện là một yếu tố quan trọng. Nếu đầu vào không được scaling có thể dẫn đến quá trình huấn luyện không ổn định. Ngoài ra nếu đầu ra Y không được scale trong các bài toán regression có thể dẫn đến exploding gradient khiến thuật toán không chạy được.
Scaling có thể tạo ra sự khác biệt giữa một mô hình kém và một mô hình tốt.
Bước tiền xử lý dữ liệu liên quan đến kỹ thuật normalization và standardization để rescale lại input và output trước khi huấn luyện mô hình.
Trong bài viết này, chúng ta sẽ tìm hiểu các để cải thiện một mô hình sao cho hiệu quả và ổn định bằng việc scale dữ liệu.
Mục tiêu bài viết
- Data scaling là một bước cần được thực hiện trong quá trình tiền xử lý khi cài đặt với mô hình mạng nơ ron
- Thực hiện được scale data bằng kỹ thuật normalization hoặc standardization.
- Áp dụng standardization và normalization để cải thiện mô hình Multilayer Perceptron với bài toán regression sau đó đưa ra đánh giá.
Scale các biến đầu vào
Các biến đầu vào là các biến đưa vào mạng neuron để dự đoán.
Một nguyên tắc chung là các biến đầu vào phải có giá trị nhỏ, có thể nằm trong khoảng 0-1 hoặc được chuẩn hóa với giá trị trung bình bằng 0 và độ lệch chuẩn (standard deviation) bằng 1. Các biến đầu vào có cần phải scaling hay không phụ thuộc vào từng bài toán cụ thể và từng biến cụ thể.
Nếu phân bố các giá trị của biến là phân bố chuẩn thì biến nên được standardization, nếu không dữ liệu nên được normalization. Điều này áp dụng khi phạm vi giá trị lớn (10, 100…) hoặc nhỏ (0.01, 0.0001).
Nếu giá trị của biến nhỏ (gần trong khoảng 0-1) và phân phối bị giới hạn (ví dụ độ lệch chuẩn gần với 1) thì chúng ta không cần phải scale dữ liệu.
Các bài toán có thể phức tạp hoặc không rõ ràng nên ta không xác định được việc sử dụng kỹ thuật nào để scale dữ liệu là tốt nhất. Vì thế nên thường thì mình hay thử nghiệm scale dữ liệu và không scale có khác biệt nhau thế nào bằng việc cho mô hình chạy rồi tiến hành đánh giá.
Scale biến đầu ra
Biến đầu ra Y là biến được dự đoán bởi mô hình.
Chúng ta cần đảm bảo là giá trị của Y phải khớp với phạm vi biểu diễn của hàm kích hoạt (activation function) trong lớp output của mô hình mạng nơ-ron.
Nếu đầu ra của activation function thuộc vào miền [0, 1] thì giá trị biến đầu ra Y cũng phải nằm trong miền giá trị này. Tuy nhiên chúng ta nên chọn hàm kích hoạt phù hợp với phân bố của đầu ra Y hơn là đưa Y về miền giá trị của hàm kích hoạt.
Ví dụ nếu bài toán của bạn là regression thì đầu ra sẽ là một giá trị số thực. Mô hình tốt nhất cho bài toán này đó là lựa chọn hàm kích hoạt tuyến tính (linear activation). Nếu đầu ra có phân bố chuẩn thì chúng ta có thể standardize biến đầu ra. Nếu không thì đầu ra Y có thể được normalize.
Các phương pháp data scaling
Có 2 cách để scale dữ liệu đó là normalization và standardization tạm dịch là Bình thường hóa dữ liệu và Chuẩn hóa dữ liệu
Cả 2 cách này đều được cung cấp trong thư viện scikit-learn
Data Normalization
Normalization là phương pháp scale dữ liệu từ miền giá trị bất kì sang miền giá trị nằm trong khoảng 0 đến 1.
Phương pháp này yêu cầu chúng ta cần xác định được giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của dữ liệu.
Giá trị được normalize theo công thức sau:
1
y = (x - min) / (max - min)
y là biến sau normalize, x là biến trước normalize.
Để normalize dữ liệu, ta cần normalize từng thuộc tính (feature) của dữ liệu. Công thức trên áp dụng đối với từng feature.
Trong đó x là giá trị cần được normalize, maximum và minium là giá trị lớn nhất và nhỏ nhất của trong tất cả các quan sát của feature trong tập dữ liệu.
Ví dụ với một tập dữ liệu bất kỳ, chúng ta xác định được giá trị lớn nhất của 1 feature là 30, giá trị nhỏ nhất là -10. Như vậy, với 1 giá trị bất kỳ là 18.8, ta có thể normalize như sau:
1
2
3
4
y = (x - min) / (max - min)
y = (18.8 - (-10)) / (30 - (-10))
y = 28.8 / 40
y = 0.72
Bạn có thể thấy nếu giá trị x nằm ngoài giới hạn của giá trị minimum và maximum, giá trị kết quả sẽ không nằm trong phạm vi 0 và 1. Nếu đã xác định giá trị max và min cho trước, một điểm dữ liệu nào đó nằm ngoài khoảng max và min đó ta có thể loại bỏ khỏi tập dữ liệu.
Bạn có thể thực hiện normalize dữ liệu sử dụng thư viện scikit-learn với MinMaxScaler.
Các bước như sau:
- Fit biến scaler sử dụng tập dữ liệu huấn luyện. Để normalize thì dữ liệu huấn luyện cần phải được xác định giá trị max và min. Để thực hiện chúng ta gọi hàm fit().
- Tiến hành scale dữ liệu bằng cách gọi hàm transform().
- Áp dụng lại bộ scaler để sử dụng cho việc dự đoán về sau.
Bộ scaler MinMaxScaler sẽ đưa các biến về miền giá trị [0, 1], sử dụng tham số feature_range để đưa vào giá trị min và max nếu bạn muốn.
1
2
# create scaler
scaler = MinMaxScaler(feature_range=(-1,1))
Để đảo ngược miền giá trị sau khi scale về miền giá trị gốc giúp thuận tiện cho việc báo cáo hay vẽ biểu đồ, bạn có thể gọi hàm inverse_transform.
1
2
3
4
5
6
7
8
9
10
11
12
# Ví dụ về scale sử dụng MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
# Load dữ liệu
data = ...
# tạo bộ scaler
scaler = MinMaxScaler()
# fit scaler vào data
scaler.fit(data)
# Thực hiện scale
normalized = scaler.transform(data)
# quay lại miền giá trị cũ
inverse = scaler.inverse_transform(normalized)
Bạn cũng có thể thực hiện trong một bước duy nhất bằng cách sử dụng hàm fit_transform (); ví dụ:
1
2
3
4
5
6
7
8
9
10
# Ví dụ về scale sử dụng MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
# load data
data = ...
# tạo bộ scaler
scaler = MinMaxScaler()
# fit và transform đồng thời
normalized = scaler.fit_transform(data)
# quay lại miền giá trị cũ
inverse = scaler.inverse_transform(normalized)
Data Standardization
Chuẩn hóa dữ liệu là việc scale dữ liệu về một phân bố trong đó giá trị trung bình của các quan sát bằng 0 và độ lệch chuẩn = 1. Kỹ thuật này còn được gọi là “whitening.”. Nhờ việc chuẩn hóa, các thuật toán như linear regression, logistic regression được cải thiện.
Công thức chuẩn hóa như sau:
\[x’ = \frac{x - \bar{x}}{\sigma}\]với $\bar{x}$ và $\sigma$ lần lượt là kỳ vọng và phương sai (standard deviation) của thành phần đó trên toàn bộ training data.
(theo https://machinelearningcoban.com/general/2017/02/06/featureengineering/)
Giống như normalization, standardization có thể có hiệu quả và thậm chí bắt buộc nếu giá trị dữ liệu đầu vào thuộc vào các miền giá trị khác nhau.
Standardization giả định các quan sát có phân phối Gaussian (dạng hình chuông). Nếu phân phối dữ liệu không có dạng phân phối chuẩn thì việc áp dụng standardize cũng không hiệu quả.
Để thực hiện standardize dữ liệu, chúng ta cần tính được giá trị trung bình và độ lệch chuẩn dựa trên các quan sát.
Công thức chuẩn hóa:
1
y = (x - mean) / standard_deviation
Trong đó mean được tính như sau:
1
mean = sum(x) / count(x)
Để tính độ lệch chuẩn (standard_deviation):
1
standard_deviation = sqrt( sum( (x - mean)^2 ) / count(x))
Giả sử giá trị trung bình là 10, độ lệch chuẩn là 5, Với giá trị 20.7 sẽ được chuẩn hóa như sau:
1
2
3
4
y = (x - mean) / standard_deviation
y = (20.7 - 10) / 5
y = (10.7) / 5
y = 2.14
Chúng ta có thể chuẩn hóa dữ liệu bằng thư viện scikit-learn với StandardScaler:
1
2
3
4
5
6
7
8
9
10
11
12
# demonstrate data standardization with sklearn
from sklearn.preprocessing import StandardScaler
# load data
data = ...
# create scaler
scaler = StandardScaler()
# fit scaler on data
scaler.fit(data)
# apply transform
standardized = scaler.transform(data)
# inverse transform
inverse = scaler.inverse_transform(standardized)
Hoặc sử dụng hàm fit_transform như sau:
1
2
3
4
5
6
7
8
9
10
# demonstrate data standardization with sklearn
from sklearn.preprocessing import StandardScaler
# load data
data = ...
# create scaler
scaler = StandardScaler()
# fit and transform in one step
standardized = scaler.fit_transform(data)
# inverse transform
inverse = scaler.inverse_transform(standardized)
Thử nghiệm với bài toán sử dụng mô hình hồi quy
Một bài toán sử dụng mô hình dự báo hồi quy thường liên quan đến việc dự đoán một đại lượng có giá trị thực. Ví dụ bài toán dự đoán giá nhà, dự đoán giá cổ phiếu…
Trong phần này, chúng ta sẽ khảo sát các loss function phù hợp cho các bài toán regression.
Để tạo dữ liệu demo cho bài toán regression, mình sẽ sử dụng hàm make_regression() có sẵn trong thư viện của scikit-learn. Hàm này sẽ tạo dữ liệu mẫu với các biến đầu vào, nhiễu và các thuộc tính khác…
Chúng ta sẽ sử dụng hàm này để tạo ra dữ liệu gồm 20 features, 10 features có ý nghĩa về mặt dữ liệu và 10 features không có ý nghĩa. Mình sẽ tạo 1,000 điểm dữ liệu ngẫu nhiên cho bài toán. Tham số random_state sẽ đảm bảo cho chúng ta các dữ liệu là như nhau mỗi lần chạy.
1
2
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
Các biến đầu vào đều dưới dạng phân phối Gaussian. Tương tự với biến đầu ra.
Mình sẽ vẽ thử biểu đồ các biến đầu vào:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# regression predictive modeling problem
from sklearn.datasets import make_regression
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# histograms of input variables
pyplot.subplot(211)
pyplot.hist(X[:, 0])
pyplot.subplot(212)
pyplot.hist(X[:, 1])
pyplot.show()
# histogram of target variable
pyplot.hist(y)
pyplot.show()
Chạy thử đoạn code trên sẽ cho chúng ta 2 kết quả như sau:
- Đầu tiên là phân bố của 2 biến trong số 12 biến:
Phân bố của 2 biến trong số 12 biến
- Thứ 2 là phân bố của biến mục tiêu. Mặc dù miền giá trị rộng hơn nhưng phân bố vẫn dưới dạng phân bố chuẩn.
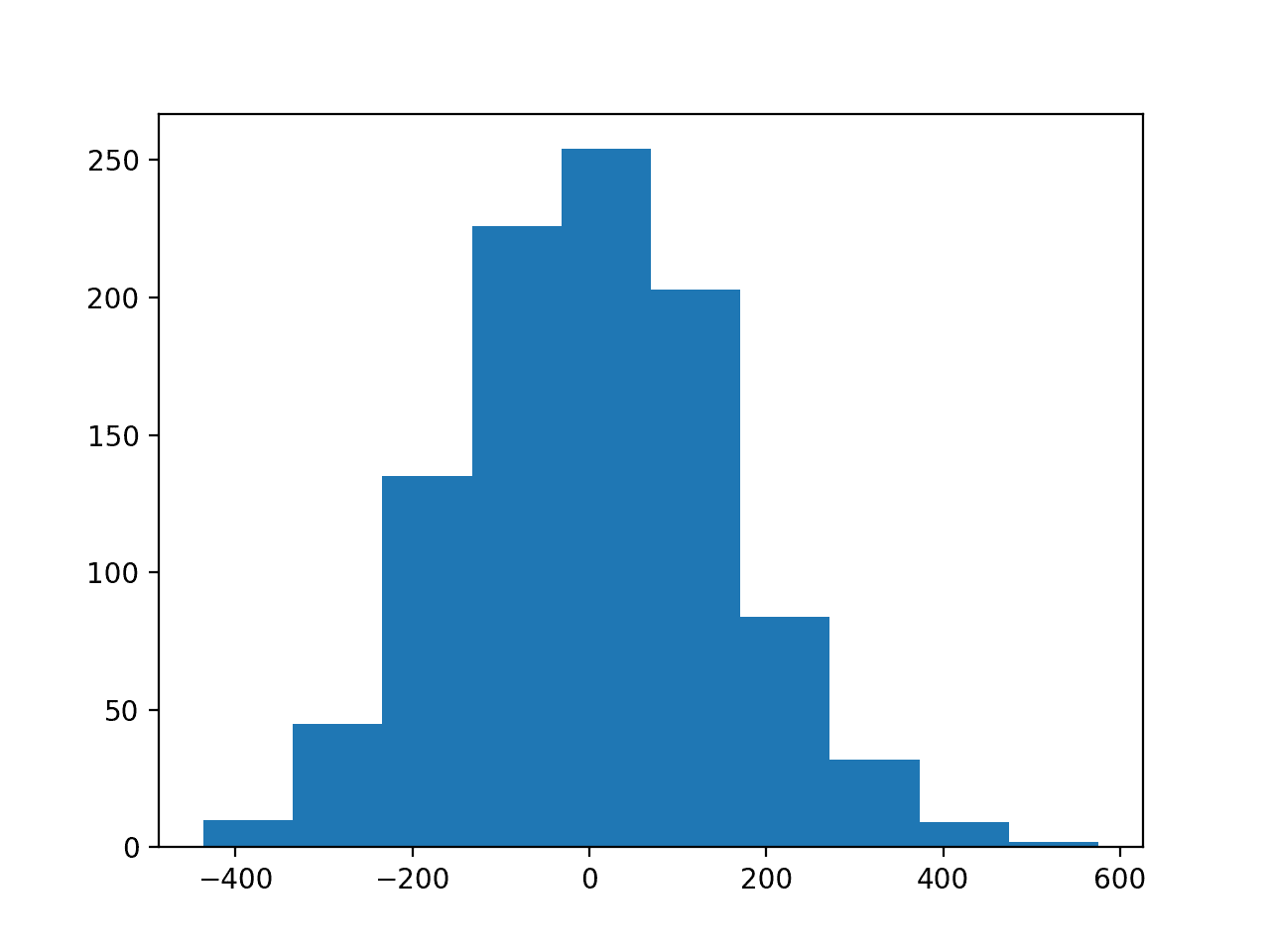Phân bố của biến mục tiêu
Như vậy chúng ta sẽ sử dụng mô hình để tiến hành các thử nghiệm và đánh giá.
MLP với dữ liệu chưa được rescale
Để demo việc tìm hiểu về sự ảnh hưởng của scaling, mình sẽ sử dụng một model đơn giản đó là Multilayer Perceptron (MLP).
Model sẽ gồm đầu vào là 20 features, mô hình sẽ có 1 lớp ẩn với 25 nodes, sau đó sử dụng hàm kích hoạt ReLU. Đầu ra sẽ gồm 1 node tương ứng với giá trị đầu ra muốn dự đoán, cuối cùng sẽ là một hàm kích hoạt tuyến tính .
1
2
3
4
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
Mình sẽ fit mô hình này với thuật toán tối ưu stochastic gradient descent và sử dụng learning rate là 0.01, momentum 0.9
Việc huấn luyện sẽ thực hiện qua 100 epochs và sử dụng tập testing để đánh giá mô hình sau mỗi epoch. Cuối cùng ta có thể vẽ lại được learning curves sau khi thực hiện xong.
1
2
3
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9))# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
Hàm lỗi MSE (mean squared error) được tính toán trên tập huấn luyện và tập kiểm tra để xác định xem mô hình học thế nào.
1
2
3
# đánh giá mô hình
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
Sau đó mình sẽ tiến hành vẽ lại biểu đồ thể hiện lỗi MSE trong quá trình huấn luyện dựa trên tập train và tập test thông qua mỗi epoch. Việc đánh giá kết quả huấn luyện dựa trên biểu đồ sẽ giúp chúng ta dễ dàng tìm hiều hơn về các thử nghiệm.
1
2
3
4
5
6
# plot loss during training
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
Code hoàn chỉnh như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# mlp with unscaled data for the regression problem
from sklearn.datasets import make_regression
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9))
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy code, chúng ta sẽ có giá trị MSE trên tập train và tập test.
Trong trường hợp này, mô hình không học được gì cả, dẫn đến giá trị dự đoán là NaN. Các trọng số của mô hình bị explode trong quá trình huấn luyện do giá trị mất mát lớn ảnh hưởng đến việc cập nhật trọng bằng Gradient descent.
1
Train: nan, Test: nan
Như vậy việc scale dữ liệu là hoàn toàn cần thiết khi xây dựng mô hình.
Do giá trị lỗi là NaN nên trong trường hợp này ta không thể vẽ được đồ thị hàm lỗi.
MLP với việc scale biến mục tiêu
Chúng ta sẽ tiến hành cập nhật lại mô hình bằng cách scale lại biến đầu ra y của tập dữ liệu.
Khi đưa biến mục tiêu về cùng miền giá trị sẽ làm giảm kích thước gradient để cập nhật lại trọng số. Điều này sẽ làm mô hình và quá trình huấn luyện ổn định hơn.
Với biến mục tiêu có phân phối Gausian, chúng ta sẽ sử dụng phương pháp thay đổi tỉ lệ giá trị của biến bằng kỹ thuật standardize. Chúng ta cần tính giá trị trung bình (mean) và độ lệch chuẩn (std) của biến để áp dụng phương pháp này.
Thư viện scikit-learn cần đầu vào dữ liệu là 1 ma trận 2 chiều gồm các dòng và các cột. Vì vậy biến mục tiêu Y từ ma trận 1D phải được reshape về 2D.
1
2
3
# reshape 1d arrays to 2d arrays
trainy = trainy.reshape(len(trainy), 1)
testy = testy.reshape(len(trainy), 1)
Sau đó áp dụng StandardScaler vào để scale lại biến:
1
2
3
4
5
6
7
8
# created scaler
scaler = StandardScaler()
# fit scaler on training dataset
scaler.fit(trainy)
# transform training dataset
trainy = scaler.transform(trainy)
# transform test dataset
testy = scaler.transform(testy)
Sau đó tương tự như phần trên, chúng ta sẽ tiến hành phân tích lỗi MSE thông qua đồ thị biểu diễn lỗi trong quá trình huấn luyện
Code thực hiện như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# mlp with scaled outputs on the regression problem
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# reshape 1d arrays to 2d arrays
trainy = trainy.reshape(len(trainy), 1)
testy = testy.reshape(len(trainy), 1)
# created scaler
scaler = StandardScaler()
# fit scaler on training dataset
scaler.fit(trainy)
# transform training dataset
trainy = scaler.transform(trainy)
# transform test dataset
testy = scaler.transform(testy)
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9))
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy, kết quả sẽ in ra giá trị MSE trên tập train và tập test
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Kết quả in ra sẽ là:
1
Train: 0.003, Test: 0.007
Biểu đồ đường thể hiện giá trị MSE trong quá trình huấn luyện của tập train (màu xanh) và tập test (màu cam)
Trong trường hợp này chúng ta có thể thấy mô hình nhanh chóng học được dữ liệu. Kết quả độ lỗi trên tập test và tập train khá tốt và gần nhau chứng tỏ mô hình không bị underfit hay overfit.
Biểu đồ đường Mean Squared Error dựa trên tập huấn luyện và kiểm tra
Perceptron nhiều lớp với việc scale biến đầu vào
Chúng ta nhận thấy việc scale dữ liệu làm ổn định quá trình huấn luyện và khớp với mô hình sau khi scale biến mục tiêu sang miền giá trị 0-1.
Ngoài ra chúng ta có thể cải thiện chất lượng mô hình bằng cách scale lại các biến đầu vào.
Mình sẽ so sánh hiệu quả của mô hình đối với việc không scale dữ liệu và scale dữ liệu bằng lần lượt 2 phương pháp standardize and normalize các biến đầu vào
Hàm get_dataset() dưới đây sẽ tiến hành tạo dữ liệu, scale và chia thành 2 tập dành cho testing và training:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# prepare dataset with input and output scalers, can be none
def get_dataset(input_scaler, output_scaler):
# generate dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# scale inputs
if input_scaler is not None:
# fit scaler
input_scaler.fit(trainX)
# transform training dataset
trainX = input_scaler.transform(trainX)
# transform test dataset
testX = input_scaler.transform(testX)
if output_scaler is not None:
# reshape 1d arrays to 2d arrays
trainy = trainy.reshape(len(trainy), 1)
testy = testy.reshape(len(trainy), 1)
# fit scaler on training dataset
output_scaler.fit(trainy)
# transform training dataset
trainy = output_scaler.transform(trainy)
# transform test dataset
testy = output_scaler.transform(testy)
return trainX, trainy, testX, testy
Tiếp theo mình sẽ định nghĩa hàm để fit MLP model vào tập dữ liệu tương ứng và trả về giá trị MSE trên tập test.
Hàm evaluate_model() được viết như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
# fit and evaluate mse of model on test set
def evaluate_model(trainX, trainy, testX, testy):
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9))
# fit model
model.fit(trainX, trainy, epochs=100, verbose=0)
# evaluate the model
test_mse = model.evaluate(testX, testy, verbose=0)
return test_mse
Neural network được huấn luyện dựa trên thuật toán stochastic. Vì vậy nên với cùng 1 dữ liệu, kết quả thực hiện có thể khác nhau. Như vậy để đánh giá chính xác chúng ta cần lặp lại nhiều lần sau đó lấy giá trị trung bình.
Hàm repeated_evaluation() sẽ thực hiện 30 lần sau đó trả về danh sách các giá trị MSE của mỗi lần chạy
1
2
3
4
5
6
7
8
9
10
11
# evaluate model multiple times with given input and output scalers
def repeated_evaluation(input_scaler, output_scaler, n_repeats=30):
# get dataset
trainX, trainy, testX, testy = get_dataset(input_scaler, output_scaler)
# repeated evaluation of model
results = list()
for _ in range(n_repeats):
test_mse = evaluate_model(trainX, trainy, testX, testy)
print('>%.3f' % test_mse)
results.append(test_mse)
return results
Cuối cùng chúng ta có thể thực nghiệm và đánh giá với cùng 1 model dựa trên 3 cách
- Không thực hiện scale đầu vào, chuẩn hóa biến đầu ra.
- Normalize đầu vào, chuẩn hóa biến đầu ra.
- Chuẩn hóa đầu vào, chuẩn hóa biến đầu ra.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# unscaled inputs
results_unscaled_inputs = repeated_evaluation(None, StandardScaler())
# normalized inputs
results_normalized_inputs = repeated_evaluation(MinMaxScaler(), StandardScaler())
# standardized inputs
results_standardized_inputs = repeated_evaluation(StandardScaler(), StandardScaler())
# summarize results
print('Unscaled: %.3f (%.3f)' % (mean(results_unscaled_inputs), std(results_unscaled_inputs)))
print('Normalized: %.3f (%.3f)' % (mean(results_normalized_inputs), std(results_normalized_inputs)))
print('Standardized: %.3f (%.3f)' % (mean(results_standardized_inputs), std(results_standardized_inputs)))
# plot results
results = [results_unscaled_inputs, results_normalized_inputs, results_standardized_inputs]
labels = ['unscaled', 'normalized', 'standardized']
pyplot.boxplot(results, labels=labels)
pyplot.show()
Code hoàn chỉnh như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# compare scaling methods for mlp inputs on regression problem
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import mean
from numpy import std
# prepare dataset with input and output scalers, can be none
def get_dataset(input_scaler, output_scaler):
# generate dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# scale inputs
if input_scaler is not None:
# fit scaler
input_scaler.fit(trainX)
# transform training dataset
trainX = input_scaler.transform(trainX)
# transform test dataset
testX = input_scaler.transform(testX)
if output_scaler is not None:
# reshape 1d arrays to 2d arrays
trainy = trainy.reshape(len(trainy), 1)
testy = testy.reshape(len(trainy), 1)
# fit scaler on training dataset
output_scaler.fit(trainy)
# transform training dataset
trainy = output_scaler.transform(trainy)
# transform test dataset
testy = output_scaler.transform(testy)
return trainX, trainy, testX, testy
# fit and evaluate mse of model on test set
def evaluate_model(trainX, trainy, testX, testy):
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9))
# fit model
model.fit(trainX, trainy, epochs=100, verbose=0)
# evaluate the model
test_mse = model.evaluate(testX, testy, verbose=0)
return test_mse
# evaluate model multiple times with given input and output scalers
def repeated_evaluation(input_scaler, output_scaler, n_repeats=30):
# get dataset
trainX, trainy, testX, testy = get_dataset(input_scaler, output_scaler)
# repeated evaluation of model
results = list()
for _ in range(n_repeats):
test_mse = evaluate_model(trainX, trainy, testX, testy)
print('>%.3f' % test_mse)
results.append(test_mse)
return results
# unscaled inputs
results_unscaled_inputs = repeated_evaluation(None, StandardScaler())
# normalized inputs
results_normalized_inputs = repeated_evaluation(MinMaxScaler(), StandardScaler())
# standardized inputs
results_standardized_inputs = repeated_evaluation(StandardScaler(), StandardScaler())
# summarize results
print('Unscaled: %.3f (%.3f)' % (mean(results_unscaled_inputs), std(results_unscaled_inputs)))
print('Normalized: %.3f (%.3f)' % (mean(results_normalized_inputs), std(results_normalized_inputs)))
print('Standardized: %.3f (%.3f)' % (mean(results_standardized_inputs), std(results_standardized_inputs)))
# plot results
results = [results_unscaled_inputs, results_normalized_inputs, results_standardized_inputs]
labels = ['unscaled', 'normalized', 'standardized']
pyplot.boxplot(results, labels=labels)
pyplot.show()
Sau khi chạy, code sẽ in ra giá trị lỗi MSE qua mỗi lần chạy.
Sau khi một trong số ba bộ tham số được đánh giá 30 lần, các lỗi trung bình cho mỗi cấu hình được in ra.
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Trong trường hợp này chúng ta có thể thấy rằng việc scale biến đầu vào sẽ làm mô hình tốt hơn. Hơn nữa việc normalize các biến đầu vào cho kết quả tốt hơn standardize. Điều này có thể do việc lựa chọn activation function là linear
1
2
3
4
5
6
7
8
9
...
>0.010
>0.012
>0.005
>0.008
>0.008
Unscaled: 0.007 (0.004)
Normalized: 0.001 (0.000)
Standardized: 0.008 (0.004)
Further Reading
Posts
- How to Scale Data for Long Short-Term Memory Networks in Python
- How to Scale Machine Learning Data From Scratch With Python
- How to Normalize and Standardize Time Series Data in Python
- How to Prepare Your Data for Machine Learning in Python with Scikit-Learn
Books
- Section 8.2 Input normalization and encoding, Neural Networks for Pattern Recognition, 1995.
API
- sklearn.datasets.make_regression API
- sklearn.preprocessing.MinMaxScaler API
- sklearn.preprocessing.StandardScaler API