Như chúng ta đã thảo luận từ các bài trước, một vài thuật toán hồi quy có thể được sử dụng để phân lớp (và ngược lại) đều cho kết quả khá tốt. Logistic Regression (hay còn gọi là Logit Regression) được sử dụng phổ biến để ước lượng xác suất 1 điểm dữ liệu có thể thuộc về 1 lớp nào đó (ví dụ tính xác suất để 1 email là spam). Nếu xác suất > 50% thì mô hình dự đoán có thể khẳng định được điểm dữ liệu đó thuộc về lớp 1 (nhãn là 1) hoặc ngược lại (nhãn là 0). Việc này được gọi là phân loại nhị phân (chỉ có 0 với 1)
Ước lượng xác suất
Làm thế nào để ước lượng được xác suất 1 điểm dữ liệu thuộc vào lớp nào? giống như mô hình hồi quy tuyến tính, mô hình hồi quy Logistic sẽ tính tổng các tích trọng số (weighted sum) với features đầu vào (có cộng thêm bias). Nhưng thay vì trả kết quả trực tiếp giống mô hình Linear Regression thì nó sẽ đi qua 1 hàm logistic để cho kết quả.
\[\hat p = h_θ(x) = σ(x^Tθ) (\text{Hàm ước lượng xác suất})\]Trong đó σ(·) là hàm sigmoid, đầu ra của nó sẽ là khoảng giá trị từ 0 đến 1.
\[\sigma(t) = \frac{1}{1 + exp(-t)}\]Chúng ta nhận xét đây là một hàm số đặc biệt, với mọi giá trị của t, hàm luôn nằm trong khoảng [0,1] và có đồ thị như sau:
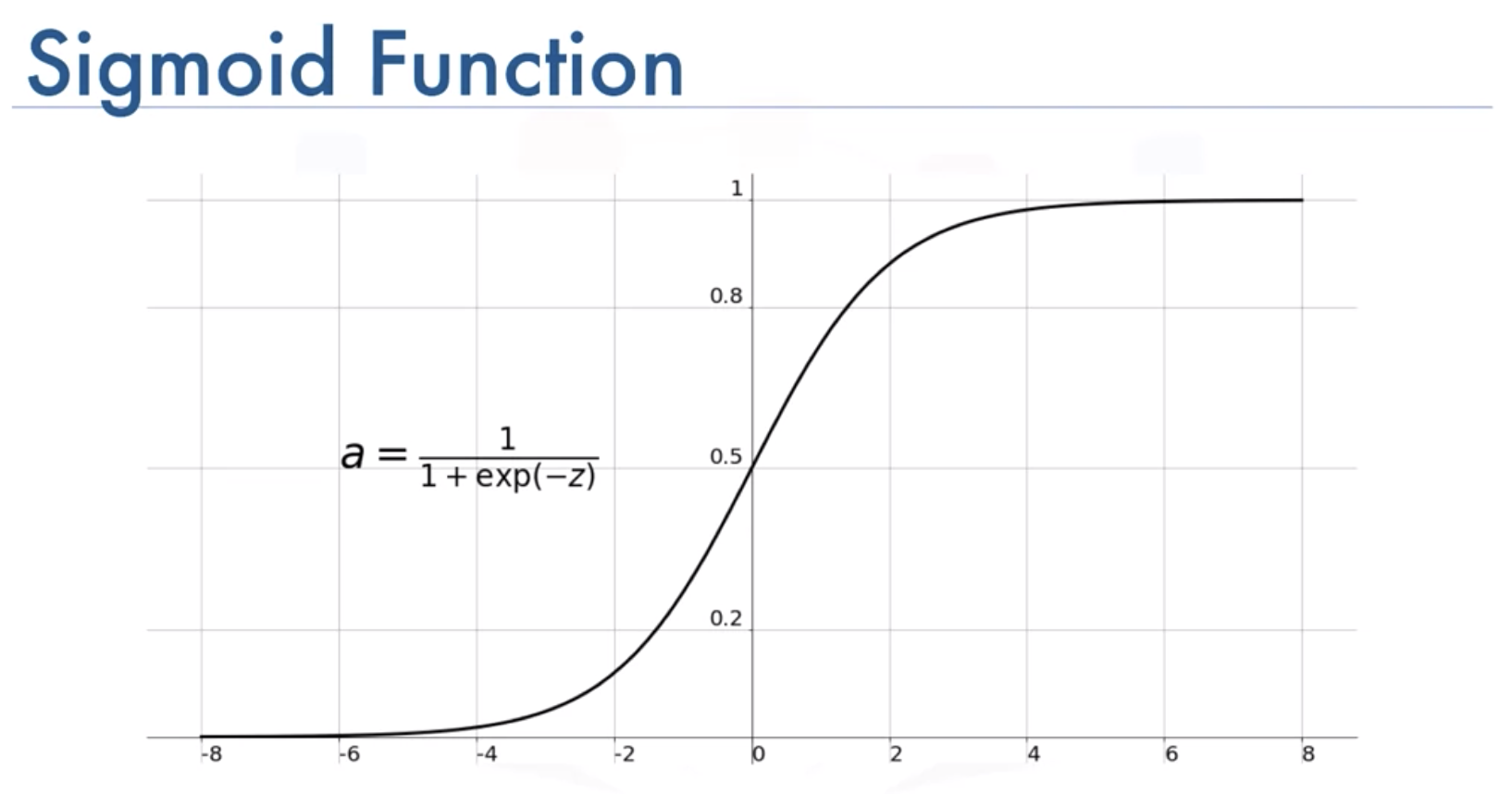Đồ thị hàm sigmoid
Sau khi đã tính được xác suất $\hat p = h_\theta(x)$ ta sẽ dễ dàng xác định được x thuộc về lớp nào, hay $\hat y$:
\[\hat y =\begin{cases}0 & \text{if $\hat p < 0.5 $} \\1 & \text{if $\hat p \ge 0.5 $}\end{cases}\]Để ý rằng $σ(t) < 0.5$ khi $t<0$ và $σ(t) \ge 0.5$ khi $t \ge 0$ vì vậy hồi quy Logistic sẽ dự đoán là 1 khi $x^T \theta$ là dương và 0 khi $x^T \theta$ âm.
Hàm chi phí và huấn luyện mô hình
Vì ta phân lớp dựa trên xác suất nên hàm chi phí sẽ được tính dựa trên xác suất xảy ra. Vì vậy mục tiêu của việc training sẽ là tìm ra vector tham số θ để mô hình ước lượng xác suất cao cho các điểm dữ liệu thuộc vào lớp 1 (positive) và xác suất thấp cho các điểm dữ liệu thuộc vào lớp 2 (negative) nên ta sẽ có hàm chi phí cho điểm dữ liệu x như sau:
\[c(\theta) =\begin{cases}-log(\hat p) & \text{if $ y = 1 $} \\-log(1- \hat p) & \text{if $ y = 0 $}\end{cases}\]Hàm chi phí rất “nhạy” bởi vì – log(t) sẽ tăng nhanh khi t xấp xỉ 0. Nếu ta dự đoán dữ liệu thuộc lớp 1 có xác xuất nhỏ thì chi phí sẽ lớn (trường hợp dự đoán sai) và nếu ta dữ đoán dữ liệu thuộc lớp 0 mà có xác suất nhỏ thì chi phí sẽ nhỏ và xấp xỉ dần về 0. Đây chính là mục tiêu của chúng ta khi huấn luyện mô hình.
Hàm chi phí trong toàn bộ tập huấn chỉ đơn giản là chi phí trung bình trên tất cả các điểm dữ liệu huấn luyện. Nên chúng ta có thể viết gộp lại thành biểu thức sau:
\[J(\theta)=-\frac{1}{m}\sum_{i=1}{m}[y^{(i)} log(\hat p^{(i)}) + (1-y^{(i)})log(1-\hat p^{(i)})]\]Ở công thức này chúng ta không thể tính được tham số θ để tối thiểu hóa hàm chi phí một cách trực tiếp. Tuy nhiên thì hàm này là hàm lồi, vì vậy nên ta có thể sử dụng Gradient Descent (hoặc bất kì thuật toán tối ưu nào) như ở bài trước để thực hiện tìm cực tiểu (nếu learning rate không quá lớn và bạn chờ đủ lâu). Đạo hàm từng phần của hàm chi phí $ \theta_j $ được tính như sau (tiến hành đạo hàm theo θ):
\[\frac{\delta J(\theta) }{\delta \theta_j}= \frac{1}{m}\sum_{1}^{m}(\sigma (\theta^Tx^{(i)}) - y^{(i)})x_j^{(i)}\]Qua mỗi điểm dữ liệu, chúng ta sẽ tính toán lỗi của việc dự đoán và nhân nó với x thứ j rồi thực hiện tính trung bình trên toàn bộ tập huấn luyện.
Khi đó chúng ta có gradient vector chứa tất cả các đạo hàm riêng để thực hiện thuật toán Batch Gradient Descent. Và theo công thức cập nhật θ chúng ta sẽ có:
$ \theta = \theta - η\frac{\delta J(\theta)}{\delta \theta} $ Với η là learning rate
Và thay vì tính toán trên toàn bộ tập huấn luyện, bạn cũng có thể sử dụng Mini-batch GD hoặc Stochastic GD như mình giới thiệu ở bài trước.
Lập trình
Mình sẽ thử lập trình với BGD, tập dữ liệu được sử dụng ở đây là dữ liệu bài tập trong khoá học ML của giáo sư Andrew Ng.
Mã nguồn các bạn có thể xem tại đây, dataset thì tại đây (https://github.com/dinhquy94/codecamp.vn/blob/master/ex2.ipynb)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# gradient descent max step
INTERATIONS = 200000
# learning rate
ALPHA = 0.001
# calc sigmoid function
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
# calc J function
def compute_cost(X, y, theta):
# number of training examples
m = y.size
# activation
h = sigmoid(np.dot(X, theta))
# cost
j = - np.sum(y * np.log(h) + (1 - y) * np.log(1 - h)) / m
return j
# implement BGD
def gradient_descent(X, y, theta, alpha, num_inters):
# number of training examples
m = y.size
jHistory = np.empty(num_inters)
for i in range(num_inters):
delta = np.dot(X.T, sigmoid(np.dot(X, theta))- y) / m
theta -= alpha * delta
jHistory[i] = compute_cost(X, y, theta)
return theta, jHistory
# train
theta, jHistory = gradient_descent(X, y, np.zeros(X.shape[1]), ALPHA, INTERATIONS)
print(theta)
# theta: [-7.45017822 0.06550395 0.05898701]
Kết quả
1
# theta: [-7.45017822 0.06550395 0.05898701]
Nguồn tham khảo: Blog Do Minh Hai