Nếu đã tìm hiểu về machine learning, chắc các bạn được nghe rất nhiều đến khái niệm hàm mất mát.
Trong các thuật toán tìm kiếm của trí tuệ nhân tạo cổ điển, hàm mất mát có thể là một hàm mục tiêu của quá trình tìm kiếm. Quá trình tìm kiếm sẽ thực hiện các thay đổi hay phương pháp di chuyển để hàm mục tiêu có giá trị nhỏ nhất hoặc giá trị chấp nhận được.
Còn trong lĩnh vực học máy, bản chất của quá trình học máy là với mỗi dữ liệu đầu vào trong quá trình huấn luyện, thuật toán sẽ tìm cách thay đổi các tham số bên trong mô hình để mô hình trở nên tốt hơn trong việc “dự đoán” ở tương lai với những dữ liệu đầu vào xấp xỉ hoặc tương tự. Việc thay đổi trọng số của mô hình thường được thực hiện bằng các thuật toán di chuyển theo độ dốc (hay còn gọi là Gradient descend).
Hàm mất mát ở đây sẽ đóng vai trò đánh giá độ “tốt” của mô hình với một bộ trọng số tương ứng. Mục đích của quá trình huấn luyện là tìm ra bộ số để độ lớn hàm mất mát (loss function) là nhỏ nhất (cực tiểu). Như vậy ta có thể coi hàm mất mát là hàm mục tiêu trong quá trình huấn luyện.
Là một phần của thuật toán tối ưu hóa, loss đối với trạng thái hiện tại của mô hình phải được ước lượng lặp lại. Điều này đòi hỏi phải lựa chọn một hàm mục tiêu, có thể được sử dụng để ước tính độ lỗi của mô hình để cập nhật các trọng số nhằm giảm lỗi trong lần đánh giá tiếp theo.
Mục tiêu
Trong thực tế việc lựa chọn hàm mất mát ảnh hưởng rất nhiều đến chất lượng của mô hình khi huấn luyện. Bài viết này sẽ cung cấp cho các bạn nội dung về các hàm mất mát hay sử dụng, so sánh và đánh giá các hàm mất mát trong một số bài toán cụ thể.
Mô hình mạng nơron học cách ánh xạ từ inputs vào output từ các examples và lựa chọn hàm mất mát phải phù hợp với từng mô hình dự đoán cụ thể, ví dụ như các bài toán như phân loại hoặc hồi quy.
Trong bài viết này, mình sẽ trình bày các hàm mất mát cho mạng nơ-ron học sâu cho các bài toán khác nhau. Nội dung bài viết gồm:
- Cách để thiết lập model cho mean squared error và các biến thể của hồi quy (regression)
- Cách thiết lập model cho cross-entropy và hàm mất mát cho bài toán binary classification.
- Cách thiết lập model cho cross-entropy và KL divergence loss functions cho bài toán multi-class classification.
Regression Loss Functions
Một bài toán sử dụng mô hình dự báo hồi quy thường liên quan đến việc dự đoán một đại lượng có giá trị thực. Ví dụ bài toán dự đoán giá nhà, dự đoán giá cổ phiếu…
Trong phần này, chúng ta sẽ khảo sát các loss function phù hợp cho các bài toán regression.
Để tạo dữ liệu demo cho bài toán regression, mình sẽ sử dụng hàm make_regression() có sẵn trong thư viện của scikit-learn. Hàm này sẽ tạo dữ liệu mẫu với các biến đầu vào, nhiễu và các thuộc tính khác…
Chúng ta sẽ sử dụng hàm này để tạo ra dữ liệu gồm 20 features, 10 features có ý nghĩa về mặt dữ liệu và 10 features không có ý nghĩa. Mình sẽ tạo 1,000 điểm dữ liệu ngẫu nhiên cho bài toán. Tham số random_state sẽ đảm bảo cho chúng ta các dữ liệu là như nhau mỗi lần chạy.
1
2
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
Mạng nơ ron nhìn chung sẽ hoạt động tốt hơn khi các giá trị dữ liệu đầu vào và đầu ra của mô hình được scale về cùng một miền giá trị. Khi đó thuật toán học sẽ hội tụ nhanh hơn việc thuôc tính dữ liệu không cùng miền giá trị. Trong bài toán này, biến target ở dạng phân phối Gaussion, do vậy việc chuẩn hóa dữ liệu rất cần thiết.
Mình sẽ sử dụng class StandardScaler trong thư viện scikit-learn. Còn trong thực tế chúng ta nên xây dựng một bộ scaler cho cả tập training và tập testing. Để đơn giản, mình sẽ scale dữ liệu trước khi chia ra làm tập train và tập test
1
2
3
# chuẩn hóa dữ liệu
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
Sau khi scale xong, chúng ta sẽ chia thành tập train và tập test:
1
2
3
4
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
Để demo việc tìm hiểu về hàm mất mát, mình sẽ sử dụng một model đơn giản đó là Multilayer Perceptron (MLP).
Model sẽ gồm đầu vào là 20 features, mô hình sẽ có 1 lớp ẩn với 25 nodes, sau đó sử dụng hàm kích hoạt ReLU. Đầu ra sẽ gồm 1 node tương ứng với giá trị đầu ra muốn dự đoán, cuối cùng sẽ là một hàm kích hoạt tuyến tính .
1
2
3
4
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
Mình sẽ fit mô hình này với thuật toán tối ưu stochastic gradient descent và sử dụng learning rate là 0.01, momentum 0.9
Việc huấn luyện sẽ thực hiện qua 100 epochs và sử dụng tập testing để đánh giá mô hình sau mỗi epoch. Cuối cùng ta có thể vẽ lại được learning curves sau khi thực hiện xong.
1
2
3
4
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
Vậy là bây giờ chúng ta đã có bài toán và mô hình, tiếp theo mình sẽ đánh giá 3 hàm mất mát phổ biến thích hợp cho các bài toán hồi quy.
Mean Squared Error Loss
Mean Square Error (MSE) hay còn được gọi là L2 Loss là một loss function cũng được sử dụng cho các mô hình hồi quy, đặc biệt là các mô hình hồi quy tuyến tính. MSE được tính bằng tổng các bình phương của hiệu giữa giá trị thực (y : target) và giá trị mà mô hình của chúng ra dự đoán (y^:predicted).
MSE có thể được sử dụng trong keras với giá trị là ‘mse‘ hoặc ‘mean_squared_error‘ khi huấn luyện mô hình
1
model.compile(loss='mean_squared_error')
MSE được ưu tiên dùng cho mô hình có layer đầu ra có 1 node và sử dụng hàm kích hoạt tuyến tính
Ví dụ:
1
model.add(Dense(1, activation='linear'))
Code hoàn chỉnh sẽ như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# Tạo dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# Chuẩn hóa dữ liệu
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# Chia tập dữ liệu training và testing
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# Định nghĩa mô hình
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_error', optimizer=opt)
# Huấn luyện mô hình
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Đánh giá mô hình
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# Vẽ lại đồ thị hàm mất mát trong quá trình huấn luyện
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy, kết quả sẽ in ra giá trị MSE trên tập train và tập test
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Kết quả in ra sẽ là:
1
Train: 0.000, Test: 0.001
Biểu đồ đường thể hiện giá trị MSE trong quá trình huấn luyện của tập train (màu xanh) và tập test (màu cam)
Kết quả huấn luyện dựa trên loss
Chúng ta có thể thấy mô hình đã hội tụ nhanh chóng. Như vậy MSE thể hiện tốt trong trường hợp này.
Mean Squared Logarithmic Error Loss
Có một vấn đề với các mô hình hồi quy, đó là giá trị dự đoán có sự chênh lệch lớn hoặc rất lớn, nghĩa là khi chúng ta dự đoán được một giá trị lớn, ta không cần phải đánh phạt trọng số một cách nặng nề (nghĩa là các trọng số không nên được thay đổi nhiều) như khi dùng MSE.
Thay vào đó, trước tiên bạn có thể lấy logarit của từng giá trị dự đoán, sau đó tính sai số bình phương trung bình. Đây được gọi là mất mát lỗi lôgarit trung bình bình phương, viết tắt là MSLE.
Nó có ý nghĩa là giảm việc phạt trọng số khi dự đoán được một giá trị lớn.
Như một phép đo sự mất mát, điều này sẽ giúp mô hình xấp xỉ tốt hơn khi dự đoán các giá trị chưa được scale. Mình sẽ chứng minh hàm mất mát này bằng một bài toán regression đơn giản:
Mình sẽ thay đổi hàm mất mát khi huấn luyện bằng hàm ‘mean_squared_logarithmic_error‘ và để nguyên các mô hình ở các layer đầu ra. Sau đó mình sẽ tính sai số bình phương trung bình để vẽ đồ thị.
1
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
Code hoàn chỉnh như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# Tạo dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# Chuẩn hóa dữ liệu
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# Chia tập dữ liệu training và testing
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# Định nghĩa mô hình
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
# Huấn luyện mô hình
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Đánh giá mô hình
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# Vẽ lại đồ thị hàm mất mát trong quá trình huấn luyện
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()
Chạy đoạn code sẽ sẽ in ra lỗi bình phương trung bình cho mô hình khi huấn luyện và tập dữ liệu thử nghiệm.
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Trong trường hợp này, chúng ta có thể thấy rằng mô hình dẫn đến MSE kém hơn một chút trên cả tập dữ liệu huấn luyện và kiểm tra. Nó có thể không phù hợp cho bài toán này vì phân phối của biến mục tiêu là một phân phối chuẩn Gaussian .
1
Train: 0.165, Test: 0.184
Biểu đồ sau thể hiện các giá trị loss MSLE qua mỗi epochs, đường màu xanh thể hiện trên tập huấn luyện, màu cam thể hiện trên tập test
Chúng ta có thể thấy rằng MSLE đã hội tụ tốt khi thực hiện được 100 epochs; còn MSE có vẻ như thay đổi quá mức, loss giảm nhanh và bắt đầu tăng từ 20 epochs trở đi.
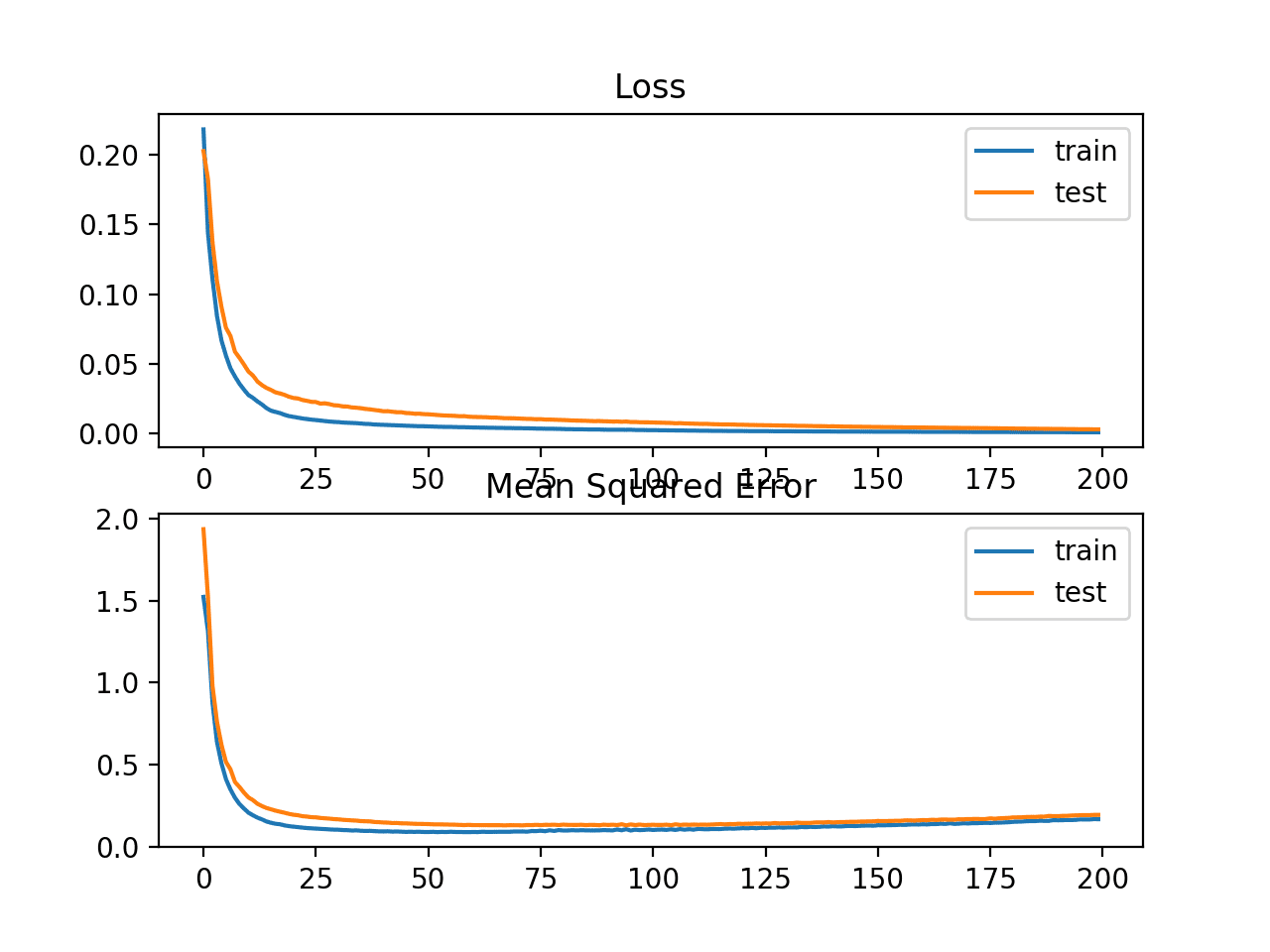Line Plots of Mean Squared Logarithmic Error Loss and Mean Squared Error Over Training Epochs
Mean Absolute Error Loss
Trong một số bài toán hồi quy, phân phối của biến mục tiêu có thể chủ yếu là phân phối Gaussian, nhưng có thể có các giá trị ngoại lệ, ví dụ: giá trị lớn hoặc nhỏ khác xa với giá trị trung bình.
Mean Absolute Error (MAE) hay còn được gọi là L1 Loss là một loss function được sử dụng cho các mô hình hồi quy, đặc biệt cho các mô hình hồi quy tuyến tính. MAE được tính bằng tổng các trị tuyệt đối của hiệu giữa giá trị thực (y : target) và giá trị mà mô hình của chúng ra dự đoán (y^: predicted).
Mình sẽ thay đổi hàm mất mát khi huấn luyện bằng hàm ‘mean_absolute_error‘ và để nguyên các mô hình ở các layer đầu ra. Sau đó mình sẽ tính sai số bình phương trung bình để vẽ đồ thị.
1
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
Code hoàn chỉnh như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# mlp for regression with mae loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()
Code sẽ in ra giá trị MLSE cho mô hình trên tập huấn luyện và tập thử nghiệm.
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
1
Train: 0.002, Test: 0.002
Trong trường hợp này, chúng ta có thể thấy rằng MAE thực sự hội tụ nhưng vẫn có đường gập ghềnh, mặc dù tổng quát của MSE không bị ảnh hưởng nhiều. Chúng ta biết rằng phân phối của biến mục tiêu là một phân phối Gaussian chuẩn không có giá trị ngoại lệ lớn, vì vậy MAE sẽ không phù hợp trong trường hợp này.
Tổng kết
Trong phần 1 mình đã giới thiệu cho các bạn 2 hàm loss được dùng cho bài toán regression, trong bài tiếp theo (p2) mình sẽ giới thiệu hàm loss cho bài toán Binary classification và phần 3 là các hàm loss cho bài toán phân đa lớp.
Tham khảo
Posts
- Soft Margin Support Vector Machine.
- Loss and Loss Functions for Training Deep Learning Neural Networks
Papers
API
- Keras Loss Functions API
- Keras Activation Functions API
- sklearn.preprocessing.StandardScaler API
- sklearn.datasets.make_regression API
- sklearn.datasets.make_circles API
- sklearn.datasets.make_blobs API