Phân lớp nhị phân là bài toán mà biến đầu ra (y) chỉ nhận một trong hai giá trị là 1 trong 2 nhãn.
Bài toán thường dưới dạng bài toán dự đoán giá trị 0 hoặc 1 cho lớp đầu tiên hoặc lớp thứ hai và thường được phát biểu như dự đoán xác suất của đầu vào thuộc giá trị lớp 1.
Trong phần này chúng ta sẽ khảo sát các hàm loss cho bài toán phân lớp nhị phân.
Chuẩn bị dữ liệu và mô hình
Mình sẽ khởi tạo dữ liệu thử nghiệm bằng thư viện scikit-learn, dữ liệu các lớp sẽ dưới dạng hình tròn. Bài toán về các vòng tròn liên quan đến các mẫu được vẽ từ hai vòng tròn đồng tâm trên một mặt phẳng hai chiều, trong đó các điểm trên vòng tròn bên ngoài thuộc lớp 0 và các điểm cho vòng tròn bên trong thuộc lớp 1. Nhiễu được thêm vào các mẫu để tránh overfit khi tìm hiểu.
Mình sẽ tạo ra 1.000 điểm dữ liệu và thêm 10% dữ liệu nhiễu . Trình tạo số giả ngẫu nhiên sẽ được thiết lập với cùng 1 giá trị tham số để đảm bảo rằng chúng ta luôn nhận được 1.000 điểm dữ liệu giống nhau ở mỗi lần chạy khác nhau.
1
2
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
Mình sẽ vẽ thử các điểm dữ liệu:
1
2
3
4
5
6
7
8
9
10
11
12
# scatter plot of the circles dataset with points colored by class
from sklearn.datasets import make_circles
from numpy import where
from matplotlib import pyplot
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# select indices of points with each class label
for i in range(2):
samples_ix = where(y == i)
pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i))
pyplot.legend()
pyplot.show()
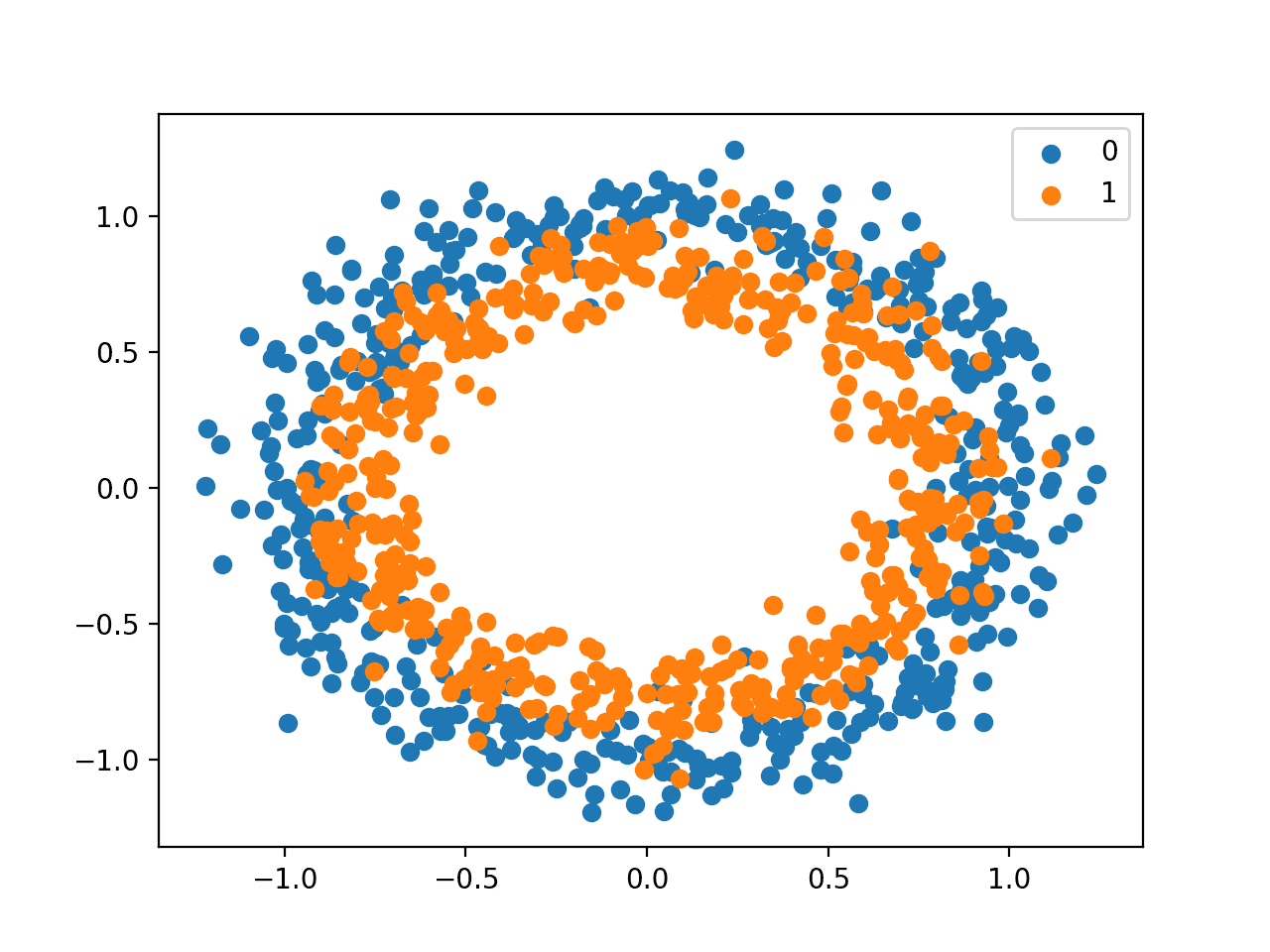Scatter Plot cho tập dữ liệu Circles Binary Classification
Các điểm dữ liệu nằm xung quanh giá trị 0, gần như trong khoảng [-1,1]. Mình sẽ không rescale chúng trong trường hợp này.
Phân chia dữ liệu huấn luyện, kiểm tra:
1
2
3
4
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
Chúng ta có thể sử dụng một mô hình MLP đơn giản để giải quyết bài toán này. Bài toán sẽ gồm đầu vào với 2 features, một lớp ẩn với 50 nút. Hàm kích hoạt tuyến tính và layer đầu ra mình sẽ lựa chọn theo mỗi hàm mất mát sẽ sử dụng.
1
2
3
4
# Định nghĩa mô hình
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='...'))
Mô hình sẽ được fit bằng thuật toán SGD với learning rate là 0.01 và momentum là 0.9
1
2
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])
Mình sẽ huấn luyện mô hình với 200 epochs sau đó đánh giá mô hình với loss và độ chính xác (accuracy) ở mỗi epoch. Sau đó mình sẽ vẽ learning curves.
1
2
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
Sau khi đã định nghĩa xong mô hình, bây giờ mình sẽ tiến hành thử nghiệm các hàm lỗi khác nhau và so sánh kết quả giữa các hàm loss để đưa ra nhận xét cho mỗi phương pháp.
Binary Cross-Entropy Loss
Cross-entropy là hàm loss được sử dụng mặc định cho bài toán phân lớp nhị phân.
Nó được thiết kế để sử dụng với bài toán phân loại nhị phân trong đó các giá trị mục tiêu nhận một trong 2 giá trị {0, 1}.
Về mặt toán học, nếu như MSE tính khoảng cách giữa 2 đại lượng số thì cross-entropy hiểu nôm na là phương pháp tính khoảng cách giữa 2 phân bố xác suất.
\[H(\mathbf{p}, \mathbf{q}) = \mathbf{E_p}[-\log \mathbf{q}]\]Với p và q là rời rạc (như y - nhãn thật sự và y^ - nhãn dự đoán ) trong bài toán của chúng ta), công thức này được viết dưới dạng:
\[H(\mathbf{p}, \mathbf{q}) =-\sum_{i=1}^C p_i \log q_i ~~~ (1)\]Trong đó C là số lượng các class cần phân lớp, trong bài toán binary classification thì C = 2.
Cross-entropy được cung cấp trong Keras bằng cách thiết lập tham số loss=‘binary_crossentropy‘ khi compile mô hình.
1
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
Hàm yêu cầu layer đầu ra được gồm 1 node và sử dụng kích hoạt ‘sigmoid’ để dự đoán xác suất cho đầu ra.
1
model.add(Dense(1, activation='sigmoid'))
Code đầy đủ sử dụng hàm loss Cross-entropy được trình bày dưới đây:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# mlp for the circles problem with cross entropy loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# Tạo bộ dữ liệu 2 chiều cần phân lớp
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# định nghĩa mô hình
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# huấn luyện mô hình
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# Đánh giá mô hình
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# Vẽ đồ thị hàm loss
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# Vẽ đồ thị độ chính xác
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy, kết quả sẽ in ra độ chính xác trên tập train và tập test
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Kết quả in ra sẽ là:
1
Train: 0.836, Test: 0.852
Trong trường hợp này chúng ta có thể thấy mô hình đạt độ chính xác 83% trên tập dữ liệu huấn luyện và 85% trên tập test. Kết quả độ chính xác trên tập test và tập train khá gần nhau chứng tỏ mô hình không bị underfit hay overfit.
Biểu đồ đường thể hiện giá trị cross-entropy trong quá trình huấn luyện của tập train (màu xanh) và tập test (màu cam)
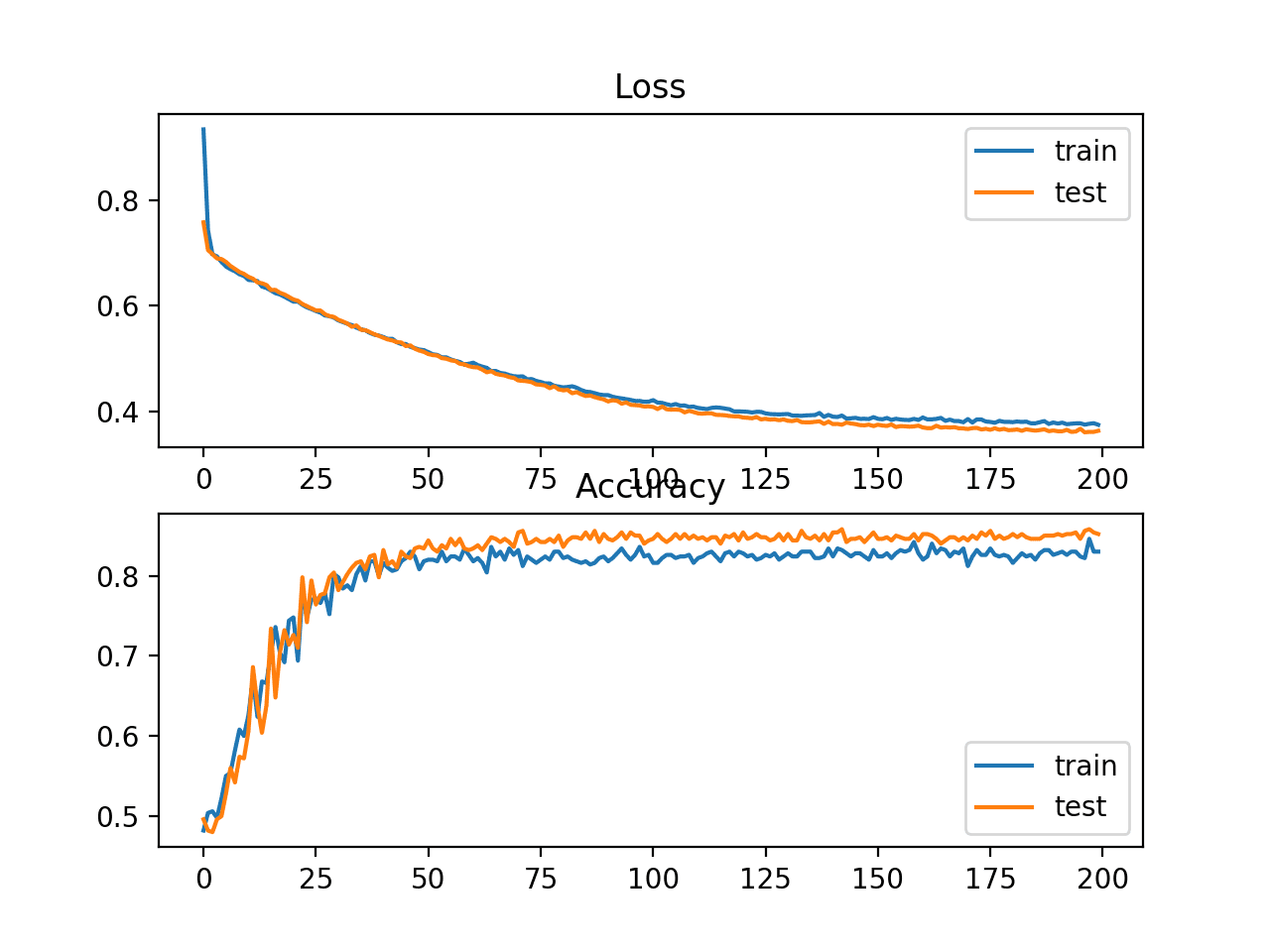Đồ thị đường của hàm mất mát Cross Entropy và độ chính xác
Khi nào sử dụng cross-entropy?
- Bài toán phân lớp
- Tạo ra các mô hình với độ chắc chắn cao (precision, recall cao)
Hinge Loss
Một cách khác để tính cross-entropy cho bài toán phân lớp nhị phân đó là hàm hinge loss. Đây là ý tưởng chính của mô hình Support Vector Machine (SVM).
Nó được thiết kế để sử dụng với bài toán phân loại nhị phân trong đó các giá trị mục tiêu nhận một trong 2 giá trị {-1, 1}.
\[J_n(\mathbf{w}, b) = \max(0, 1 - y_nz_n)\]Trong đó, $z_n$có thể được coi là score của $x_n$ ứng với cặp hệ số $(\mathbf{w}, b)$ chính là đầu ra mong muốn.
Hàm loss sẽ khuyến khích các điểm dữ liệu có dấu đúng, phạt lỗi nặng hơn nếu có giá trị dự đoán có dấu khác với giá trị mong muốn.
Trong thực tế, hinge loss thường thể hiện tốt hơn cross-entropy trong các bài toán binary classification
Đầu tiên, chúng ta sẽ đưa các nhãn đầu ra thành một trong 2 giá trị -1 và 1
1
2
# đổi y từ {0,1} thành {-1,1}
y[where(y == 0)] = -1
Chúng ta có thể chỉ định hàm loss trong khi compile bằng giá trị loss=’hinge’
1
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
Cuối cùng, lớp đầu ra của mô hình sẽ có 1 node và sử dụng hàm kích hoạt activation=’tanh’ để đảm bảo giá trị đầu ra nằm trong khoảng [-1, 1].
1
model.add(Dense(1, activation='tanh'))
Sau đây là đoạn code hoàn chỉnh:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# Tạo dữ liệu
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# đưa y từ {0,1} thành {-1,1}
y[where(y == 0)] = -1
# Chia tập dữ liệu thành 2 tập test và train
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# định nghĩa mô hình
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
# huấn luyện mô hình
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# đánh giá mô hình
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# vẽ đồ thị giá trị loss sau khi huấn luyện
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# vẽ đồ thị giá trị độ chính xác sau khi huấn luyện
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy, kết quả sẽ in ra độ chính xác của mô hình trên tập train và tập test
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Kết quả in ra sẽ là:
1
Train: 0.792, Test: 0.740
Trong trường hợp này, chúng ta có thể thấy độ chính xác kém hơn một chút so với việc sử dụng cross-entropy, với mô hình đã chọn có độ chính xác dưới 80% trên tập huấn luyện và tập kiểm tra.
Biểu đồ đường thể hiện độ chính xác trong quá trình huấn luyện của tập train (màu xanh) và tập test (màu cam)
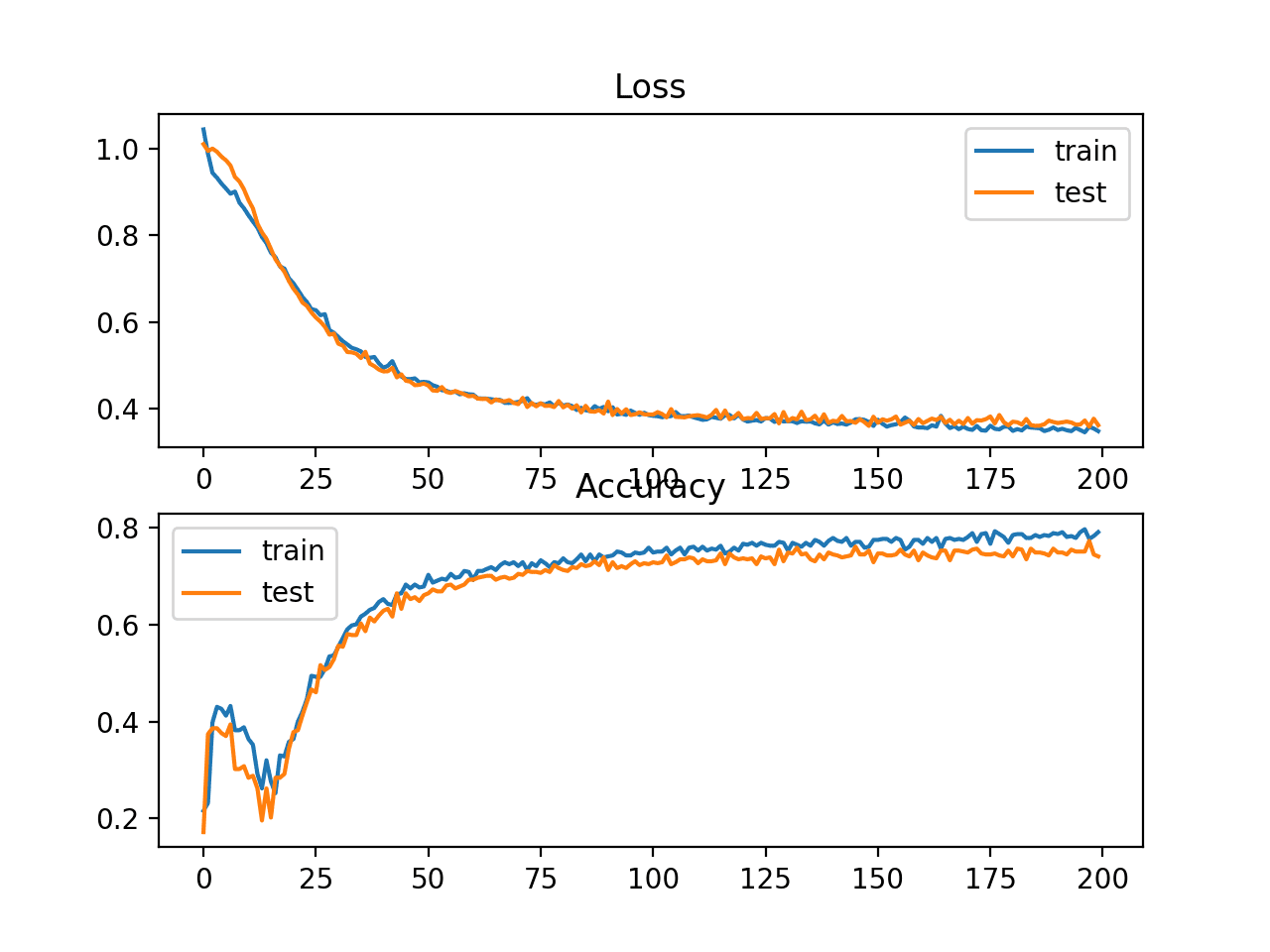Hinge Loss và Classification Accuracy
Squared Hinge Loss
Hàm hinge loss có nhiều phiên bản mở rộng, thường được sử dụng trong mô hình SVM.
Một phiên bản phổ biến của hinge loss đó là squared hinge loss. Nó có tác dụng trong việc làm giảm sự nhấp nhô của đồ thị hàm loss và dễ thao tác hơn về mặt toán học.
Nếu hàm hinge loss có kết quả tốt trong bài toán phân lớp nhị phân thì squared hinge loss cũng sẽ cho kết quả tương tự.
Giống như hinge loss, chúng ta cũng cần biến đổi các nhãn về giá trị -1 và 1.
1
2
# đổi y từ {0,1} thành {-1,1}
y[where(y == 0)] = -1
Chúng ta có thể chỉ định hàm loss trong khi compile bằng tham số
1
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
Cuối cùng, lớp đầu ra của mô hình sẽ có 1 node và sử dụng hàm kích hoạt activation=’tanh’ để đảm bảo giá trị đầu ra nằm trong khoảng [-1, 1].
1
model.add(Dense(1, activation='tanh'))
Sau đây là đoạn code hoàn chỉnh:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# Tạo dữ liệu
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# đưa y từ {0,1} thành {-1,1}
y[where(y == 0)] = -1
# Chia tập dữ liệu thành 2 tập test và train
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# định nghĩa mô hình
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
# huấn luyện mô hình
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# đánh giá mô hình
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# vẽ đồ thị giá trị loss sau khi huấn luyện
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# vẽ đồ thị giá trị độ chính xác sau khi huấn luyện
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
Sau khi chạy, kết quả sẽ in ra độ chính xác của mô hình trên tập train và tập test
Chú ý khi chạy, kết quả có thể khác nhau do thuật toán khởi tạo ngẫu nhiên. Chúng ta nên chạy nhiều lần và lấy giá trị trung bình
Kết quả in ra sẽ là:
1
Train: 0.682, Test: 0.646
Trong trường hợp này, chúng ta có thể thấy độ chính xác kém hơn một chút so với việc sử dụng Hinge loss, với mô hình đã chọn có độ chính xác dưới 70% trên tập huấn luyện và tập kiểm tra.
Biểu đồ đường thể hiện độ chính xác trong quá trình huấn luyện của tập train (màu xanh) và tập test (màu cam)
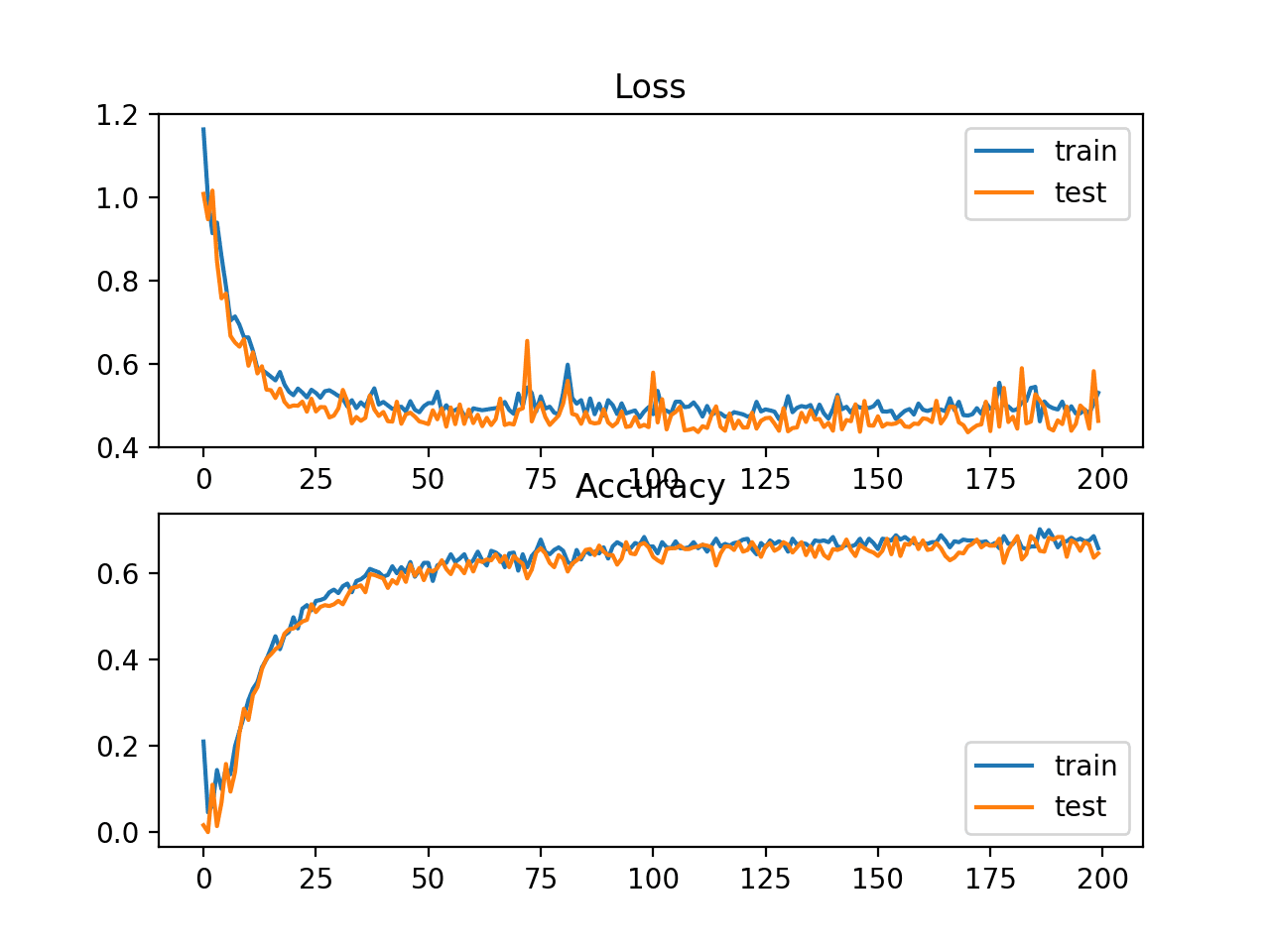Squared Hinge Loss và Classification Accuracy
Mô hình có vẻ đã hội tụ, tuy nhiên bề mặt hàm lỗi còn nhiều nhấp nhô, chứng tỏ việc thay đổi trọng số nhỏ ảnh hưởng lớn đến độ lỗi của mô hình.
Tổng kết
Trong phần 2 mình đã giới thiệu cho các bạn 2 hàm loss được dùng cho bài toán phân lớp nhị phân, trong bài tiếp theo (p3) mình sẽ giới thiệu hàm loss cho bài toán Multi-Class Classification. (phân nhiều lớp)
Tham khảo
Posts
- Soft Margin Support Vector Machine.
- Loss and Loss Functions for Training Deep Learning Neural Networks
Papers
API
- Keras Loss Functions API
- Keras Activation Functions API
- sklearn.preprocessing.StandardScaler API
- sklearn.datasets.make_regression API
- sklearn.datasets.make_circles API
- sklearn.datasets.make_blobs API