Trong bài viết này mình sẽ nói đến bài toán phân lớp và các phương pháp đánh giá 1 hệ thống phân lớp.
Mình sẽ sử dụng bộ dữ liệu MNIST, gồm 70.000 ảnh nhỏ của các số viết tay bởi người ở US. Mỗi ảnh được đánh nhãn với số tương ứng. Tập dữ liệu này được dùng cực kì phổ biến trong huấn luyện các thuật toán và thường được gọi là bộ dữ liệu “Hello World” trong Machine learning. Nói chung là ai học machine learning thì sớm hay muộn cũng phải sử dụng MNIST =))
Dữ liệu huấn luyện
Scikit-Learn cung cấp nhiều functions để tải về các bộ dữ liệu để huấn luyện. Trong đó có MNIST. Đoạn code sau đây để tải về dataset:
1
2
3
4
5
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()
dict_keys(['data', 'target', 'feature_names', 'DESCR', 'details',
'categories', 'url'])
Sau đó xem kết quả
Có 70k ảnh và mỗi ảnh có 784 features. Bởi vì mỗi ảnh có 28x28 pixels và mỗi feature đơn giản được biểu diễn bởi 1 màu từ 0 (white) đến 255 (black).
1
2
3
4
5
import matplotlib as mpl import matplotlib.pyplot as plt
some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = mpl.cm.binary, interpolation="nearest") plt.axis("off")
plt.show()
Bây giờ ta thử xem 1 vài mẫu trong tập MNIST:
 Mẫu trong tập MNIST
Mẫu trong tập MNIST
Phân chia dữ liệu
Phân chia tập dữ liệu, chúng ta sẽ tiến hành chia bộ dữ liệu ra làm 2 phần: 1 phần để training (huấn luyện) gồm 60k ảnh đầu tiên và 1 phần để đánh giá (test) gồm 10k ảnh cuối của tập dữ liệu.
1
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
Huấn luyện bộ phân lớp nhị phân (Binary Classifier)
Để cho đơn giản, chúng ta sẽ tiến hành phân lớp với 1 số, trong ví dụ này là số 5. Bộ phát hiện số 5 được gọi là 1 bộ phân lớp nhị phân (đúng hoặc sai)
Chuẩn bị dữ liệu
Bây giờ chúng ta sẽ tạo tập dữ liệu để huấn luyện:
1
2
3
# y được gán nhãn là True nếu nhãn của y là số 5, False nếu nhãn không phải số 5
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
Xây dựng và huấn luyện mô hình
Sau khi đã có tập dữ liệu để huấn luyện, bây giờ chúng ta sẽ xác định bộ phân lớp phù hợp để thực hiện phân loại. Ở bài viết này mình sử dụng bộ phân lớp Stochastic Gradient Descent (SGD)
1
2
from sklearn.linear_model import SGDClassifier sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
SGDClassifier dựa vào việc lấy ngẫu nhiên trong quá trình training (do đó được stochastic). Nếu bạn muốn kết quả không đổi sau mỗi lần chạy, bạn nên đặt thêm tham số random_state
Dự đoán kết quả sau khi huấn luyện
Sau khi huấn luyện xong chúng ta sẽ thực hiện chạy thử mô hình.
1
2
sgd_clf.predict([some_digit])
# array([ True])
Sau khi đã chạy xong việc huấn luyện mô hình, chúng ta sẽ đi vào đánh giá độ chính xác mô hình trong việc dự đoán.
Các phương pháp đánh giá mô hình dự đoán
Cross-validation.
Phương pháp tốt nhất để đánh giá 1 mô hình học máy đó là cross-validation. Cross-validation là một phương pháp kiểm tra độ chính xác của 1 máy học dựa trên một tập dữ liệu học cho trước. Thay vì chỉ dùng một phần dữ liệu làm tập dữ liệu học thì cross-validation dùng toàn bộ dữ liệu để dạy cho máy. Ở bài này mình sẽ sử dụng K-fold, đây là phương pháp dùng toàn bộ dữ liệu và chia thành K tập con. Quá trình học của máy có K lần. Trong mỗi lần, một tập con được dùng để kiểm tra và K-1 tập còn lại dùng để dạy.
1
2
3
4
5
6
7
8
9
10
from sklearn.model_selection import StratifiedKFold from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5): clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = y_train_5[train_index]
X_test_fold = X_train[test_index] y_test_fold = y_train_5[test_index]
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred)) # Lần lượt là 0.9502, 0.96565 và 0.96495
Để rút gọn thì thư viện sklearn đã cung cấp sẵn hàm để thực hiện:
1
2
3
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
# array([0.96355, 0.93795, 0.95615])
Confusion Matrix
Một phương pháp tốt hơn để đánh giá performance của mô hình phân lớp đó là confusion matrix (ma trận nhầm lẫn). Ý tưởng chính là đếm số lần phần tử thuộc class A bị phân loại nhầm vào class B.
Để thực hiện tính toán ma trận nhầm lẫn, đầu tiên bạn phải có kết quả các dự đoán và so sánh với nhãn thật của nó. Nghĩa là chúng ta phải dự đoán trên tập test, sau đó dúng kết quả dự đoán này để so sánh với nhãn ban đầu.
1
2
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
Sau đó xác định ma trận nhầm lẫn:
1
2
3
4
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
# array([[53057, 1522],
# [ 1325, 4096]])
Ma trận nhầm lẫn sẽ cho chúng ta nhiều thông tin về chất lượng của bộ phân lớp.
- TP (True Positive): Số lượng dự đoán chính xác. Là khi mô hình dự đoán đúng một số là số 5.
- TN (True Negative): Số lương dự đoán chính xác một cách gián tiếp. Là khi mô hình dự đoán đúng một số không phải số 5, tức là việc không chọn trường hợp số 5 là chính xác.
- FP (False Positive - Type 1 Error): Số lượng các dự đoán sai lệch. Là khi mô hình dự đoán một số là số 5 và số đó lại không phải là số 5
- FN (False Negative - Type 2 Error): Số lượng các dự đoán sai lệch một cách gián tiếp. Là khi mô hình dự đoán một số không phải số 5 nhưng số đó lại là số 5, tức là việc không chọn trường hợp số 5 là sai.
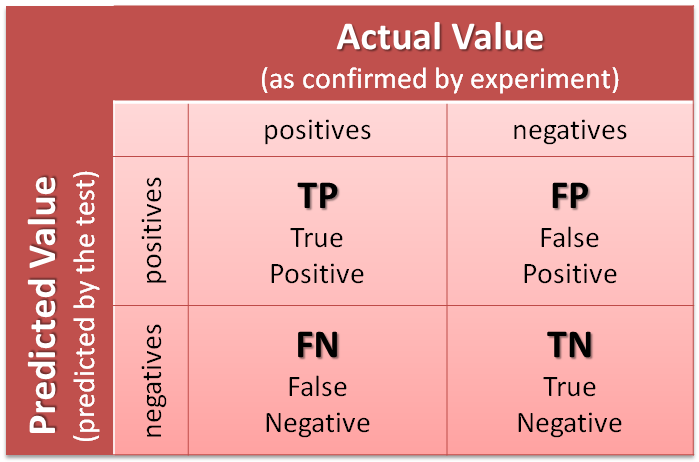 Giải thích về confusion matrix
Giải thích về confusion matrix
Từ 4 chỉ số này, ta có 2 con số để đánh giá mức độ tin cậy của một mô hình:
Precision and Recall
Precision: Trong tất cả các dự đoán Positive được đưa ra, bao nhiêu dự đoán là chính xác? Chỉ số này được tính theo công thức
precision = TP / (TP + FP)
Recall: Trong tất cả các trường hợp Positive, bao nhiêu trường hợp đã được dự đoán chính xác? Chỉ số này được tính theo công thức:
recall = TP / (TP + FN)
1
2
3
4
5
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
# == 4096 / (4096 + 1522) 0.7290850836596654
recall_score(y_train_5, y_train_pred)
# == 4096 / (4096 + 1325) 0.7555801512636044
Để kết hợp 2 chỉ số này, người ta đưa ra chỉ số F1-score
F1-score
Một mô hình có chỉ số F-score cao chỉ khi cả 2 chỉ số Precision và Recall để cao. Một trong 2 chỉ số này thấp đều sẽ kéo điểm F-score xuống. Trường hợp xấu nhất khi 1 trong hai chỉ số Precison và Recall bằng 0 sẽ kéo điểm F-score về 0. Trường hợp tốt nhất khi cả điểm chỉ số đều đạt giá trị bằng 1, khi đó điểm F-score sẽ là 1.
Để tính F1-score, ta thực hiện như sau:
1
2
3
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
# 0.7420962043663375
Tuy nhiên thì không phải lúc nào ta cũng cần đến F1, 1 vài trường hợp ta chỉ quan tâm đến precision, 1 vài trường hợp ta quan tâm đến recall. Ví dụ, nếu bạn huấn luyện 1 mô hình để phát hiện video an toàn cho trẻ em, bạn phải sử dụng bộ phân lớp mà có thể bỏ sót nhiều video an toàn (recall thấp) nhưng ít bỏ qua các video không an toàn (high precision). Hay còn gọi là giết nhầm còn hơn bỏ sót, thà không hiển thị video an toàn còn hơn là hiển thị video không an toàn.
Source Code: Các bạn có thể xem tại: https://github.com/dinhquy94/codecamp.vn/blob/master/bai3_4.ipynb
Đánh giá mô hình nhiều lớp
Trong bài này chúng ta sẽ tiếp tục với bài toán phân lớp cho nhiều lớp (multiclass classifiers), có thể phân biệt được nhiều hơn 2 lớp khác nhau.
Một vài các thuật toán (ví dụ như Random Forest hay naive Bayes) có khả năng xử lý bài toán đa lớp một cách trực tiếp. Các thuật toán khác (ví dụ như Support Vector Machine hay Linear classifiers) thì chỉ là các thuật toán phân lớp nhị phân nhưng vẫn có thể áp dụng cho bài toán phân đa lớp. Tùy vào bài toán mà chúng ta có chiến lược để sử dụng các thuật toán phân lớp khác nhau.
One-versus-all
Ví dụ để tạo ra một bộ phân lớp có thể phân loại được các ảnh của 10 chữ số (từ 0 đến 9), chúng ta sẽ phải huấn luyện 10 bộ phân lớp nhị để phát hiện ra lần lượt các chữ số (ví dụ bộ phát hiện chữ số 0, ví dụ bộ phát hiện chữ số 1, ví dụ bộ phát hiện chữ số 2…) Sau đó khi chúng ta muốn phân lớp 1 ảnh bất kì, ta sẽ đưa nó vào các bộ phát hiện này và mỗi lần thực hiện sẽ cho ra 1 decision score (khả năng xảy ra với mỗi bộ phân lớp). Sau đó kết quả sẽ là chữ số có bộ phân biệt cho kết quả decision score lớn nhất. Thuật toán này được gọi là one-versus-all (OvA - một với tất cả)
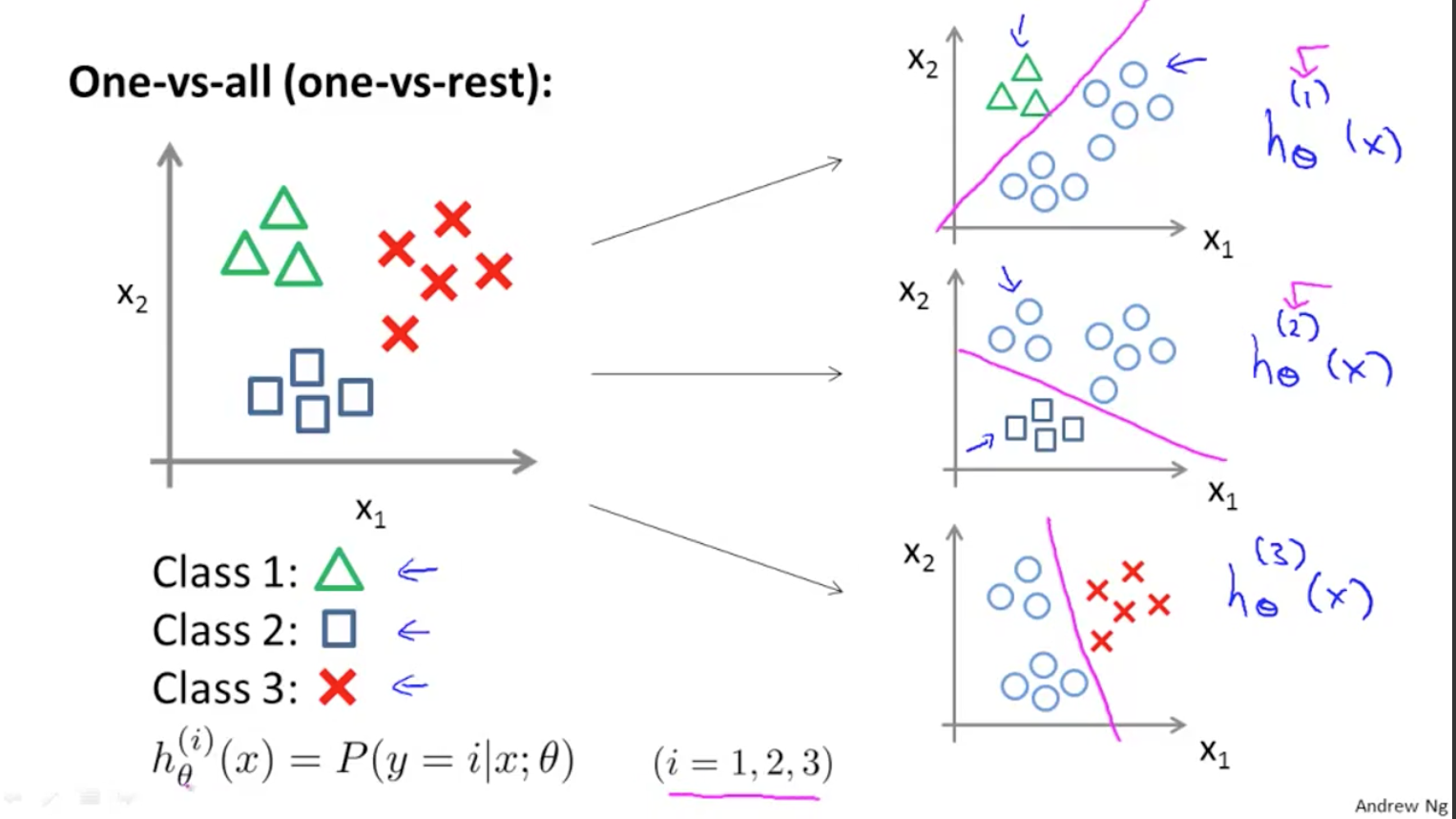 Giải thích về One-versus-all
Giải thích về One-versus-all
One-versus-one
Và 1 cách khác để tạo ra một bộ phân lớp có thể phân loại được các ảnh đó là chúng ta sẽ huấn luyện để cho mỗi số phân biệt với 10 chữ số còn lại bằng các bộ phân lớp nhị phân, như vậy mỗi số sẽ có 10 bộ phân lớp (bộ phân lớp số 1 với số 0, số 1 với số 2, số 1 với số 3…). Sau đó khi chúng ta muốn phân lớp 1 ảnh, chúng ta sẽ kết hợp kết quả của bộ dự đoán cho kết quả là True của mỗi bộ phân lớp. Đây được gọi là 1-vs-one (OvO). Nếu có N lớp thì số bộ phân lớp cần là: N × (N – 1) / 2
Trong hầu hết các thuật toán phân loại nhị phân thì OvA hay được sử dụng.
Trong thư viện Scikit-Learn, khi ta sử dụng thuật toán phân lớp nhị phân cho bài toán đa phân lớp nó sẽ tự động sử dụng thuật toán OVA để thực hiện đa phân lớp.
1
2
>>> sgd_clf.fit(X_train, y_train) # y_train, not y_train_5
>>> sgd_clf.predict([some_digit])array([5], dtype=uint8)
Đoạn code này huấn luyện mô hình phân lớp SGD trên tập huấn luyện gồm các lớp từ 0-9 (y_train) thay vì 5-vs-all (y_train_5) như ở bài trước. Về bản chất, Scikit-Learn sẽ tiến hành 10 bộ phân lớp nhị phân, sau đó lấy ra các decision score cho mỗi ảnh rồi chọn ra lớp có điểm cao nhất.
Để xem các decision scores, ta thực hiện như sau:
1
2
3
4
5
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
#array([[-15955.22627845, -38080.96296175, -13326.66694897,
# 573.52692379, -17680.6846644 , 2412.53175101, -25526.86498156,
# -12290.15704709, -7946.05205023, -10631.35888549]])
Điểm cao nhất sẽ thuộc về class 5
1
2
3
4
5
>>> np.argmax(some_digit_scores)
5
>>> sgd_clf.classes_
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8) >>> sgd_clf.classes_[5]
5
Nếu ta thực hiện phân loại với thuật toán cây ngẫu nhiên (Random Forest), thì chỉ cần thực hiện đơn giản như sau:
1
2
3
>>> forest_clf.fit(X_train, y_train)
>>> forest_clf.predict([some_digit])
array([5], dtype=uint8)
Lần này thì Random Forest sẽ không phải dùng đến 0-vs-all hoặc one-vs-one bởi vì Random Forest là thuật toán để phân lớp áp dụng cho bài toán đa phân lớp. Chúng ta có thể gọi hàm predict_proba() để lấy ra danh sách các xác suất mà mô hình phân lớp gán cho mỗi phần tử của lớp tương ứng.
1
2
>>> forest_clf.predict_proba([some_digit])
array([[0. , 0. , 0.01, 0.08, 0. , 0.9 , 0. , 0. , 0. , 0.01]])
Phân tích lỗi
Khi bạn thực hiện xong việc huấn luyện mô hình và cần phải cải thiện nó thì việc quan trọng là phải phân tích để giảm thiểu các lỗi mà nó gây ra.
Đầu tiên, bạn hãy nhìn vào ma trận nhầm lẫn. Chúng ta sẽ tiến hành dự đoán kết quả bằng hàm cross_val_predict(), sau đó gọi hàm confusion_matrix() như sau:
1
2
>>> y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3) >>> conf_mx = confusion_matrix(y_train, y_train_pred)
>>> conf_mx
array([[5578, 0, 22, 7, 8, 45, 35, 5, 222, 1],
[ 0, 6410, 35, 26, 4, 44, 4, 8, 198, 13],
[ 28, 27, 5232, 100, 74, 27, 68, 37, 354, 11],
[ 23, 18, 115, 5254, 2, 209, 26, 38, 373, 73],
[ 11, 14, 45, 12, 5219, 11, 33, 26, 299, 172],
[ 26, 16, 31, 173, 54, 4484, 76, 14, 482, 65],
[ 31, 17, 45, 2, 42, 98, 5556, 3, 123, 1],
[ 20, 10, 53, 27, 50, 13, 3, 5696, 173, 220],
[ 17, 64, 47, 91, 3, 125, 24, 11, 5421, 48],
[ 24, 18, 29, 67, 116, 39, 1, 174, 329, 5152]])
 confusion matrix
confusion matrix
Có nhiều số và thực sự là rất rối mắt để quan sát, vì vậy hãy biểu diễn nó sử dụng Matplotlib:
1
2
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
Hình này sẽ cho ta thấy các số phân loại vào đúng lớp của nó. Tuy nhiên nhìn kĩ thì có số 5 dường như có màu xám hơn so với các số còn lại. Điều này lý giải là có ít số 5 trong dataset được phân loại vào hoặc mô hình phân loại số 5 không tốt bằng các số khác. Trong trường hợp này là cả 2 khả năng đều có thể xảy ra.
Phân tích 1 cách kỹ hơn, chúng ta sẽ lấy lại công bằng cho trường hợp có ít hay nhiều số 5 hơn trong dataset, ta sẽ thực hiện chia các giá trị của confusion matrix cho tổng số các ảnh trong lớp đó, sau đó ta có thể so sánh các tỷ lệ lỗi giữa các lớp:
1
2
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
Tiếp theo chúng ta sẽ thay đường chéo bằng các số 0 để chỉ quan tâm đến tỷ lệ lỗi:
1
2
3
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
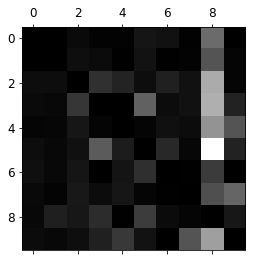
Quan sát kỹ hình ảnh này, phần tử cột thứ 8, hàng thứ 5 có màu sáng nhất so với các ô còn lại. Điều này cho ta thấy số 5 bị phân loại nhầm thành số 8 nhiều nhất (giá trị lỗi cao).
Qua bài này mình đã giới thiệu với mọi người 2 phương pháp để phân đa lớp trong machine learining và cách biểu diễn để phân tích lỗi cho các bài toán phân lớp. Bài sau mình sẽ giới thiệu các bạn bài toán gán nhiều nhãn cho 1 đối tượng.
Code của bài này các bạn có thể xem tại: https://github.com/dinhquy94/codecamp.vn/blob/master/bai3_4.ipynb
